VaryLab is all about mesh optimization, we say discrete surface optimization. That means we modify a given mesh to have minimal energy in a certain sense. The energy in question is a combination of energies that is usually defined on the vertex positions of the input mesh. This post shows you how to optimize a mesh with VaryLab. It is a very simple example that illustrates the basic steps.
1. Import and Analysis
In this example we optimize a planarity measure of quadrilateral faces. We start with a quad-mesh and a maximum relative face non-planarity of 8.1%. You can download the model here if you like to follow this example.
The Halfedge Data Visualization panel contains a data source for for planarity. You can add a node color visualizer and a histogram to the list of active visualizations. Here we adjust the color map to red-green for the node colors and the histogram such that we can compare the model and the values in the data view. The histogram visualizer has a parameter for the number of bins to use, we set it to 40.
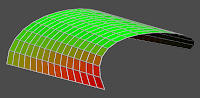
The model is a bent and twisted part of cylinder with almost planar quadrilaterals on the top and non-planar quad at the boundary. We have to decide on the goals of the optimization. In this case we want to keep the structure of the mesh and modify positions of all vertices.
 2. Optimization Configuration
2. Optimization Configuration
To begin optimization of the active mesh we have to select the energies that contribute to the energy used by the optimization core. The optimizer plug-ins panel holds a list of all available energies. If you use VaryLab online service you probably have only the energies you selected before startup. In this case we select the planar quads energy and choose the volume variant from the options. This energy is the sum of the volumes of tetrahedra spanned by non-planar quadrilaterals. This sum is scaled to render the energy scale invariant.
 From the optimization panel we open the constraints sub-panel and uncheck all constraints especially the boundary should be variable. You can constrain the optimization to move the vertices only in the allowed coordinate directions. There are other more advanced constraints that can be enabled.
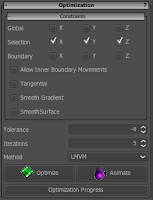
From the optimization panel we open the constraints sub-panel and uncheck all constraints especially the boundary should be variable. You can constrain the optimization to move the vertices only in the allowed coordinate directions. There are other more advanced constraints that can be enabled.A tolerance of -8 lets the optimization core optimize the energy such that the gradient norm is less than \(10^{-8}\). The number iterations stops the optimizer after the given number of optimization steps. This number depends very much on the optimization method you select in the next box. There are methods that converge slowly but achieve nicer results than other methods that minimize the energy more rapidly. In the example we choose CG as the optimization method and a number of 180 iterations to perform.
 3. Optimization
3. Optimization
 To start the optimization hit the optimize button. A new optimization job is queued in the list of jobs and started if no other jobs are waiting to be executed. You can review and manage jobs in the job monitor. Here any pending and currently running optimization job can be cancelled. The progress bar of the optimization job shows the current iteration that is performed by the optimization core. It is possible to preview the shape of the model during optimization. The animate button starts a animated optimization job that updates the positions of vertices during optimization.
To start the optimization hit the optimize button. A new optimization job is queued in the list of jobs and started if no other jobs are waiting to be executed. You can review and manage jobs in the job monitor. Here any pending and currently running optimization job can be cancelled. The progress bar of the optimization job shows the current iteration that is performed by the optimization core. It is possible to preview the shape of the model during optimization. The animate button starts a animated optimization job that updates the positions of vertices during optimization.
During optimization you can watch the optimization core doing its work in the optimization protocol panel. This panel shows a graph for every energy that is selected for optimization. Additionally, the norm of the gradient is plotted. From this information you can decide how the optimization is performing and if parameters should be adjusted. In our example we need approimately 100 iteration for the energy to drop below \(10^{-6}\) and 80 more iterations for the optimization to converge.
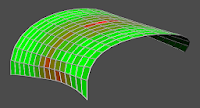
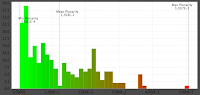 After optimization has finished the new model is shown in the view and data visualizers are updated to reflect new data. One can see for our model that optimization has changed the boundary shape drastically and faces are perfectly planar up to a tolerance of 0.02% for the most non-planar quad.
After optimization has finished the new model is shown in the view and data visualizers are updated to reflect new data. One can see for our model that optimization has changed the boundary shape drastically and faces are perfectly planar up to a tolerance of 0.02% for the most non-planar quad.


No comments:
Post a Comment